2nd Edition FX Book Projects
FXObjects: All of the projects from the 2nd edition FX book are contained in a single ZIP that includes all of the classes, functions and structures you need without any RackAFX or ASPiK code whatsoever – just pure C++: Download the FXObjects
ASPiK Projects: The projects are also formatted for the open-source ASPiK plugin framework, supported by a vibrant community of developers, keen to use and understand their own plugin framework that they control, license-free – what a fabulous group of people! This framework is updated usually on SDK releases: Download the ASPiK Projects
Below are summaries of each of the C++ fxobjects.h/.cpp plugin projects. Enjoy!
IIR Filters
- Chapter 11 Audio Filter Designs: IIR Filters
Block Diagram:
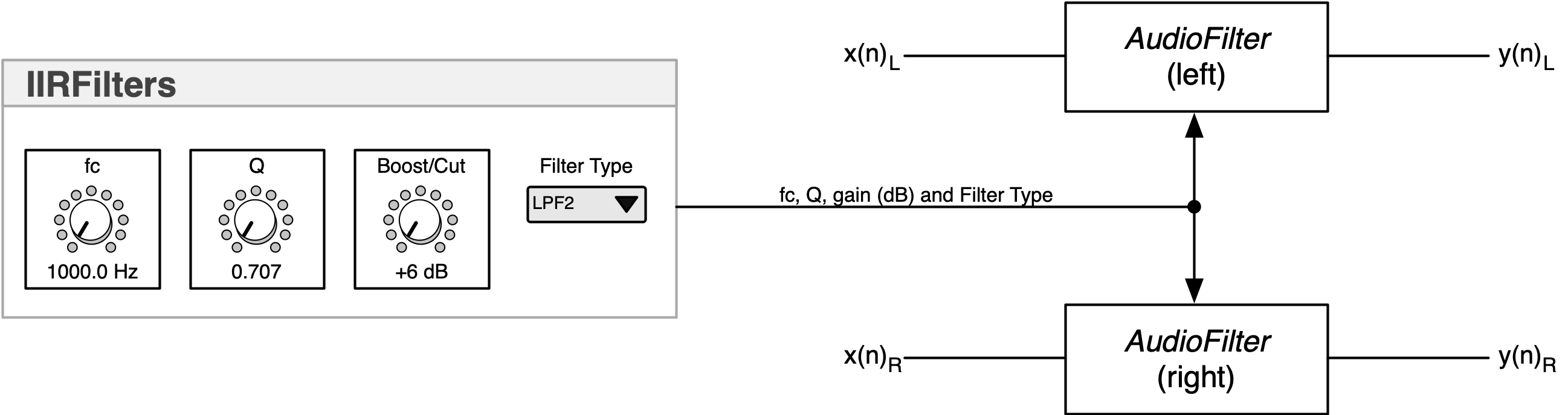
Description:
- implements all IIR filters in the 2nd edition FX book
Notes:
- this plugin implements 29 different algorithms from the book
- plus the Regalia-Mitra algorithms you add for homework
RLC Filters (WDF Library)
Designing Audio Effects Plugins in C++ 2nd Ed.
- Chapter 11 Audio Filter Designs: Wave Digital and Virtual Analog
Block Diagram: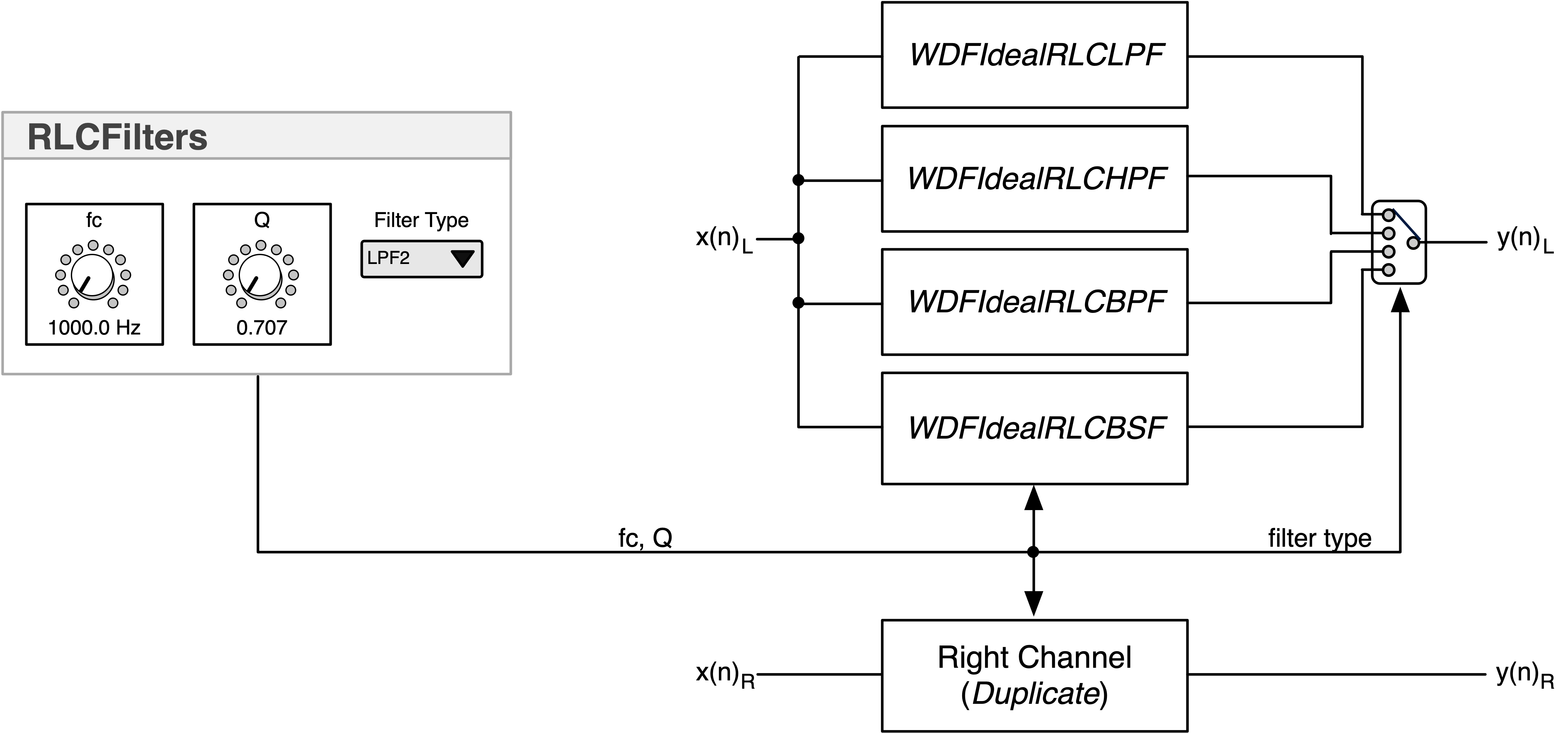
Description:
- implements the four, ideal 2nd RLC filters for LPF, HPF, BPF and BSF
- not like other WDF implementations because these require zero source impedance and infinite load impedance
- see the book above for many more details including the frequency “de-warping” that I implement
Notes:
- uses the WDF Ladder Filter Library and a separate interface specifically designed for WDFs
Modulated Filter

- Chapter 13 Modulators: LFOs and Envelope Detectors
Block Diagram:
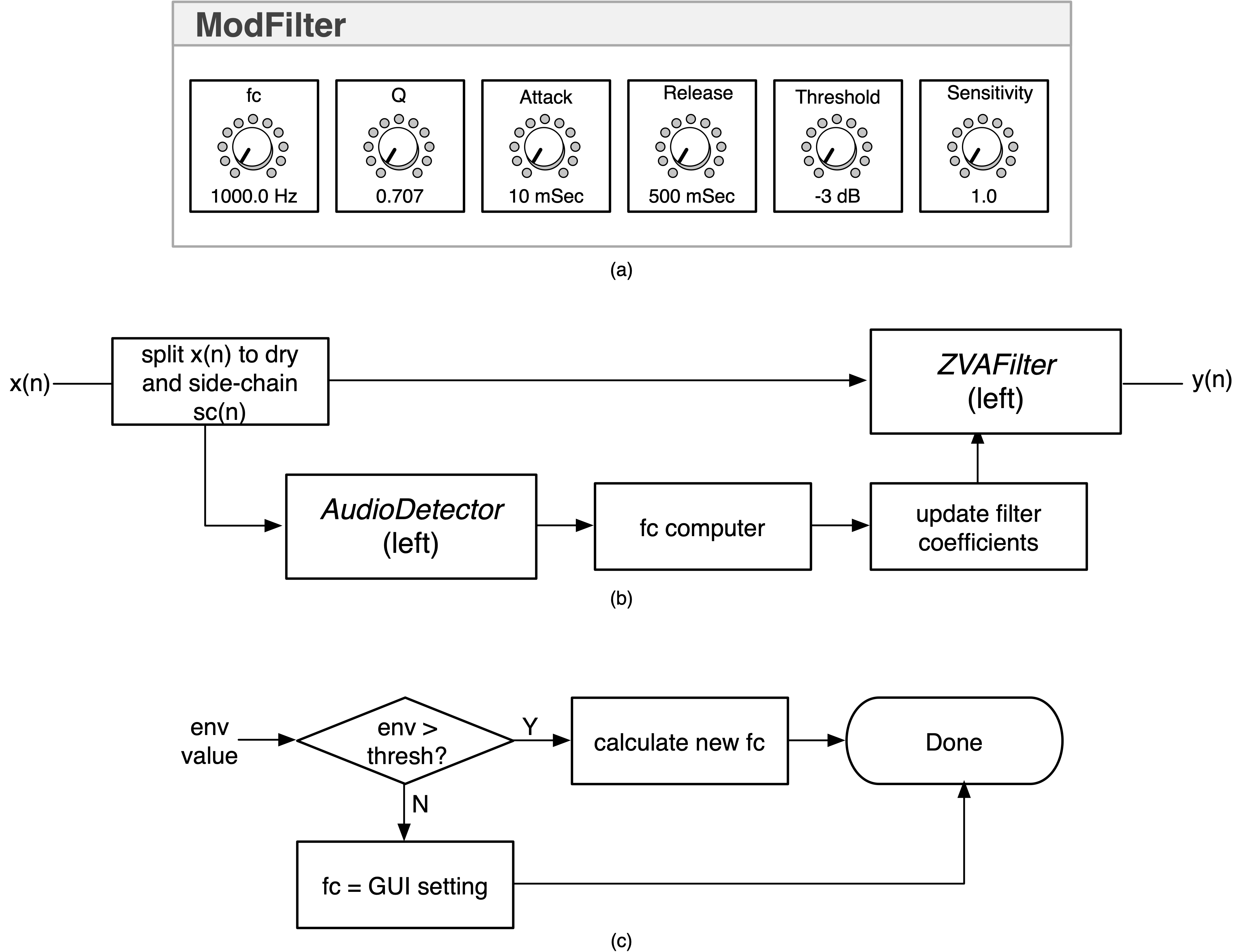
Description:
- implements a 2nd order resonant modulated LPF using the MMA LPF2 algorithm
- uses signal detection in dB and measures distances above threshold in dB
Phaser
Designing Audio Effects Plugins in C++ 2nd Ed.
- Chapter 13 Modulators: LFOs and Envelope Detectors
Bock Diagram:
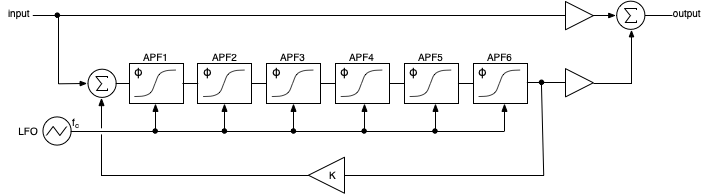
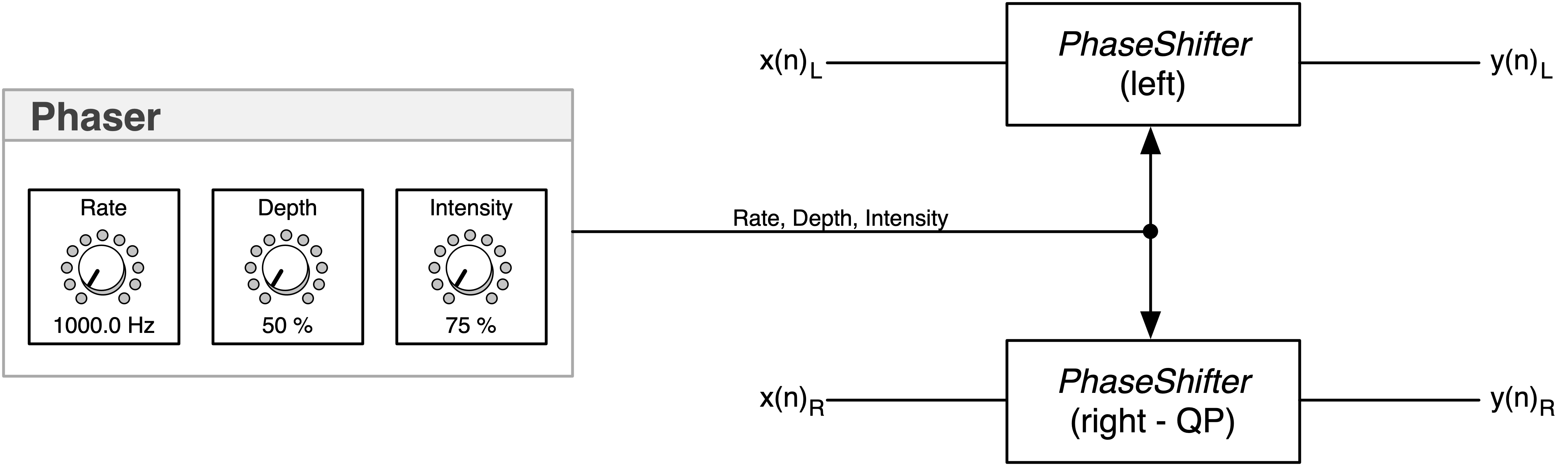
Description:
- Stereo phaser using Virtual Analog delay-free structures but based on a biquad rather than the trapezoidal integrator
- Quad-phase LFOs for double-wide stereo sound
Notes:
- you can enable the quad-phase LFO by modifying the PluginCore::updateParameters( ) method – see the commented-out code there
- you may want to set the min and max intensity (feedback in percent) values to [+70, +99] as this is the sweet-spot area for the control
Stereo Delay

Designing Audio Effects Plugins in C++ 2nd Ed.
- Chapter 14 Delay Effects and Circular Buffers
Block Diagram:
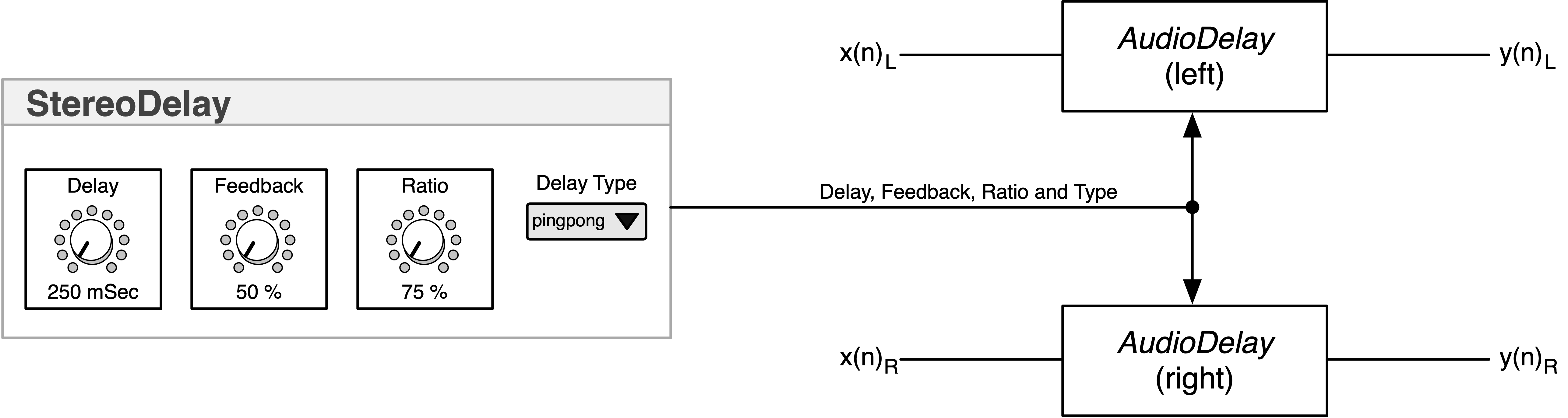
Description:
- implements normal and ping-pong delays from the book
Notes:
- processes frames or samples – your choice
- uses the delay-time-plus-ratio concept taught in the book above
NOTE: there is a newer version of this project that changes the location of the parameter update, to allow the delay control to morph smoothly as it is rotated, much like an analog delay. In addition, the newer version shows how to implement a custom preset storage and recall system and a status LED for the user.
Modulated Delay
Designing Audio Effects Plugins in C++ 2nd Ed.
- Chapter 15 Modulated Delay Effects
Block Diagram:

Description:
- implements the 3 basic modulated delays: flanger, chorus and vibrato
Notes:
- see the book for details on min and max modulation limits as these algorithms are highly customizable and highly subjective as far as these limits are concerned
- uses the Depth control to set how much of the modulated delay line is used; an alternative is to use the Depth as a wet/dry control
Analog FIR
Designing Audio Effects Plugins in C++ 2nd Ed.
- Chapter 16 Audio Filter Designs: FIR Filters
Block Diagram:
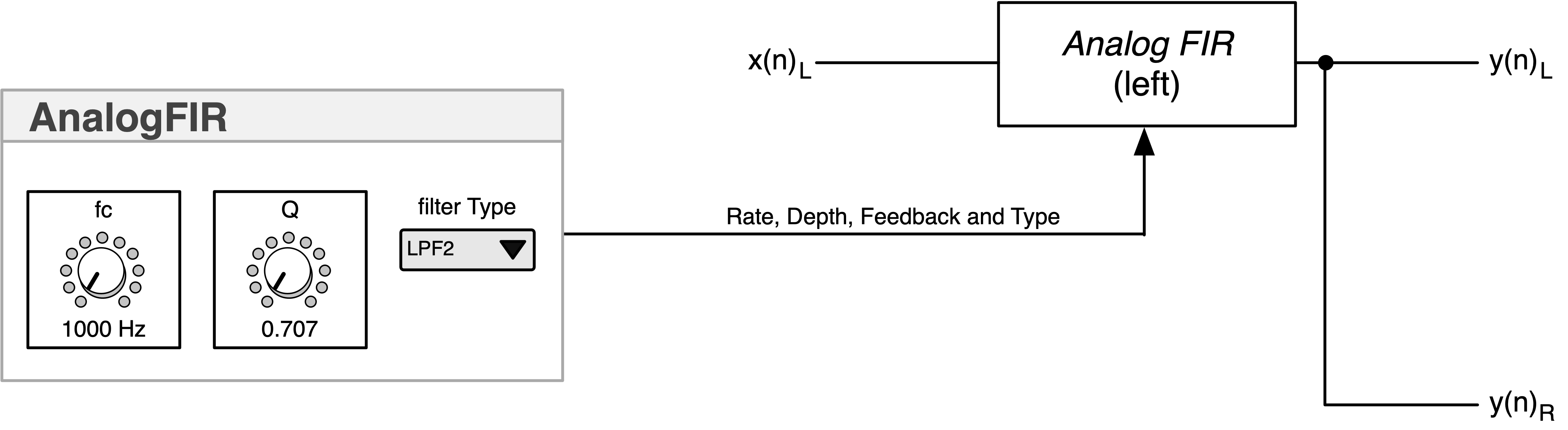
Description:
- implements analog filter responses exactly in FIR form
Notes:
- please see the book for a discussion on this plugin; I am not advocating this as a method of designing virtual analog filters
- however, the frequency response will exactly match the analog filter you specify
- and the resulting filter will also be linear phase – very interesting and bizarre kind of device here
- note that this is a mono plugin, and the GUI controls are parsed at the top of the buffer proc cycle and NOT smoothed due to the CPU-intensive nature of this algorithm
Developer Reverb
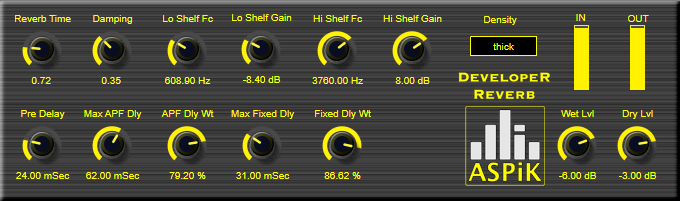
Designing Audio Effects Plugins in C++ 2nd Ed.
- Chapter 17 Reverb Effects
Block Diagram:
Description:
- this is the developer version of the Reverb plugin and is for creating new algorithms
Notes:
- See the FX book for a description of the delay and weighting method for generating sets of delaying allpass and fixed delay lines that are non-integer multiples of each other without needing 20+ GUI controls
- This version includes VU meters to monitor signal levels for algorithm development
- There are five (5) presets included for you to use as starting points for your own algorithms. They are: Tiny Room, Small Club, Bright Club, Warm Room and Large Hall
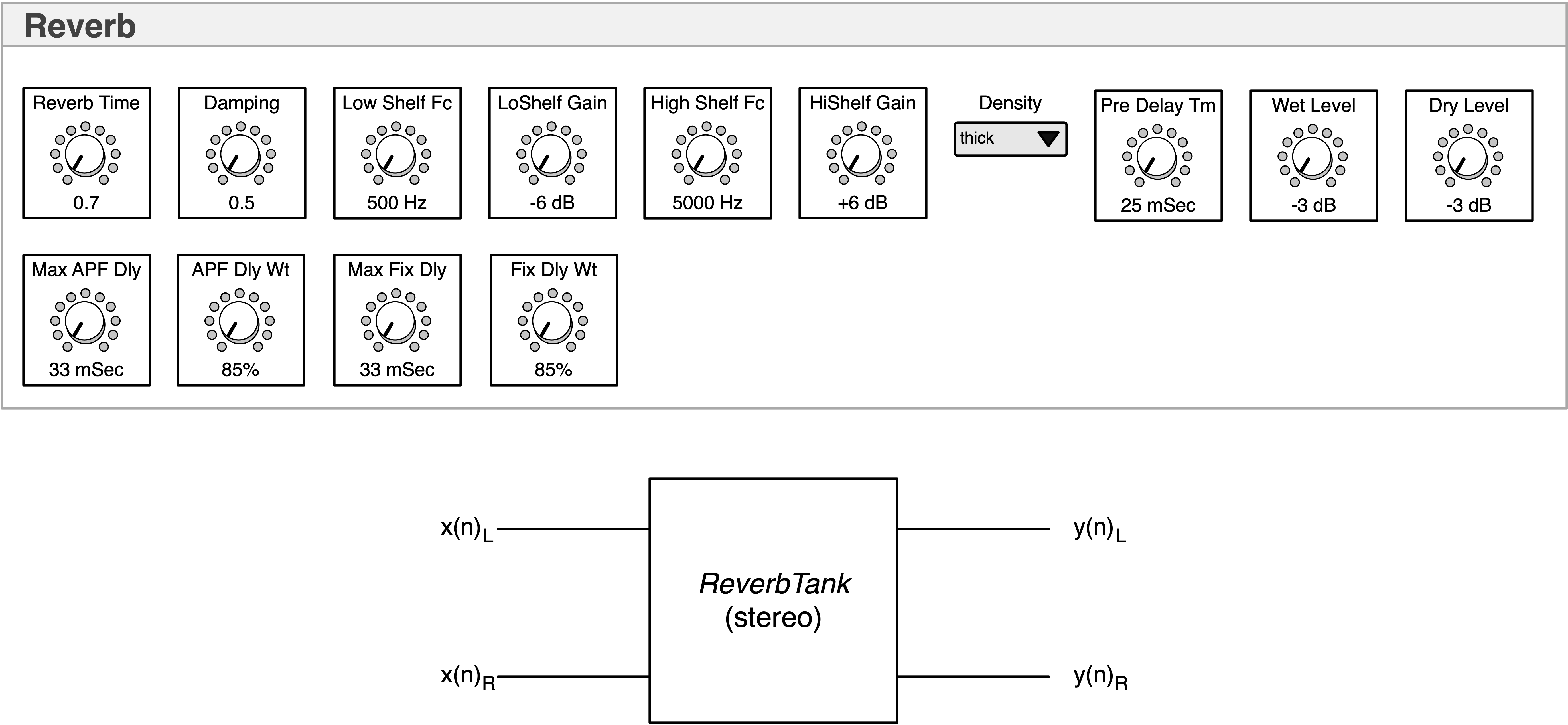
Consumer (Release) Reverb

- Chapter 17 Reverb Effects
Block Diagram: Note that this is identical to the Developer Reverb plugin – the difference is in which GUI controls are exposed for the user.

Description:
- this is the release (or consumer) version of the reverb plugin that exposes a set of presets for the user that they may tweak specialized parameters only
Notes:
- this project includes bonus material not in the text; there are two included functions that allow you to initialize the plugin from one of its own built-in presets, and another that allows you to generate a GUIParameter list based on a preset
- You can then send that GUIParameter list to the plugin shell to update the GUI from within the plugin – and YES it is threadsafe!
Dymamics

Designing Audio Effects Plugins in C++ 2nd Ed.
- Chapter 18 Dynamics Processing
Block Diagram:
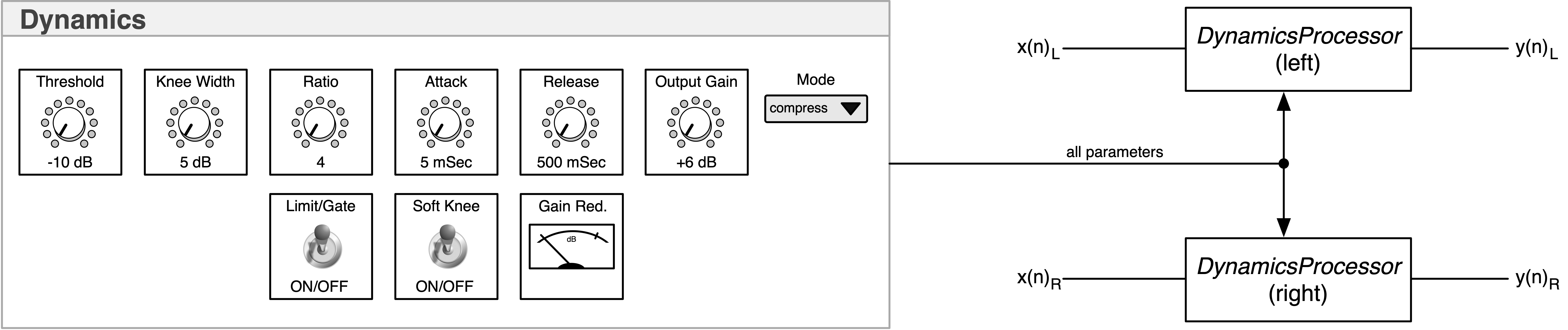
Description:
- implements the four dynamics processors compress, limit, expand, gate
Notes:
- this plugin implements an additional external sidechain for keyed effects; see the PluginCore::processAudioFrame( ) function to see how that is handled
- there is one gain reduction (upside down) meter that combines both left and right gain reduction values when running in stereo
- includes stereo link switch that was not a direct part of the book project
- includes soft-knee
Pitch Shifter

Designing Audio Effects Plugins in C++ 2nd Ed.
Block Diagram:

Description:
- stereo pitch shifter made with phase vocoders
Notes:
- includes peak tracking and phase locking options; see the text for these gory details
- requires FFTW to be installed on your system (see ASPiK documentation for instructions if you don’t know how)
- shifts pitch in semitones, but you may easily change that to be a “whammy” shifter with continuous pitch modulation
- FFTW is insanely fast so you can easily do stereo pitch shifting without much CPU usage; compile in Release mode for even faster code
Tube Preamp

NOTE: this project uses the vacuum tube models from the original book. The vacuum tube chapter was cut short due to page limits for the book. Please see the Chapter 19 Addendum, to get the missing material, PLUS a huge tutorial on vacuum tube circuit design.
Block Diagram:
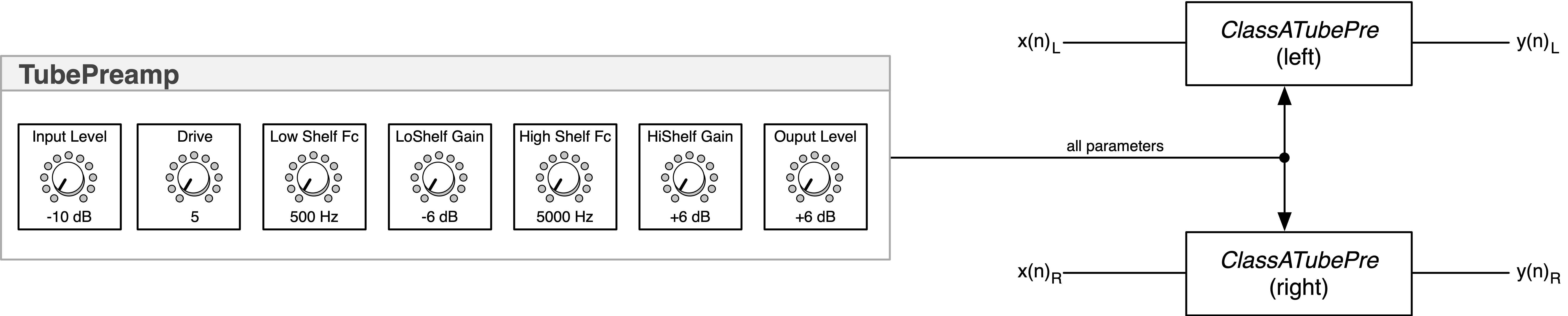
Description:
- a basic tube preamp with four class-A triode circuits
Notes:
- assumes tube drive levels are kept within proper grid voltage range; see bonus projects for grid conduction plugins (guitar amp simulator)
- designed for non-musical instrument demonstration (preamps, EQs, etc… which do not purposefully overdrive grids)
Super Saturator


Description:
- guitar distortion box emulator
Notes:
- uses the VariBPF object (see addendum) to give the nice midrangey guitar distortion we all know and love
- simple to modify for more or less distortion or to make distortion asymmetric – it is currently symmetrical in the sample project
- see the function PluginCore::guiParameterChanged( ) to see how I am handling the green LEDs on the GUI
Wicker Amp Combo
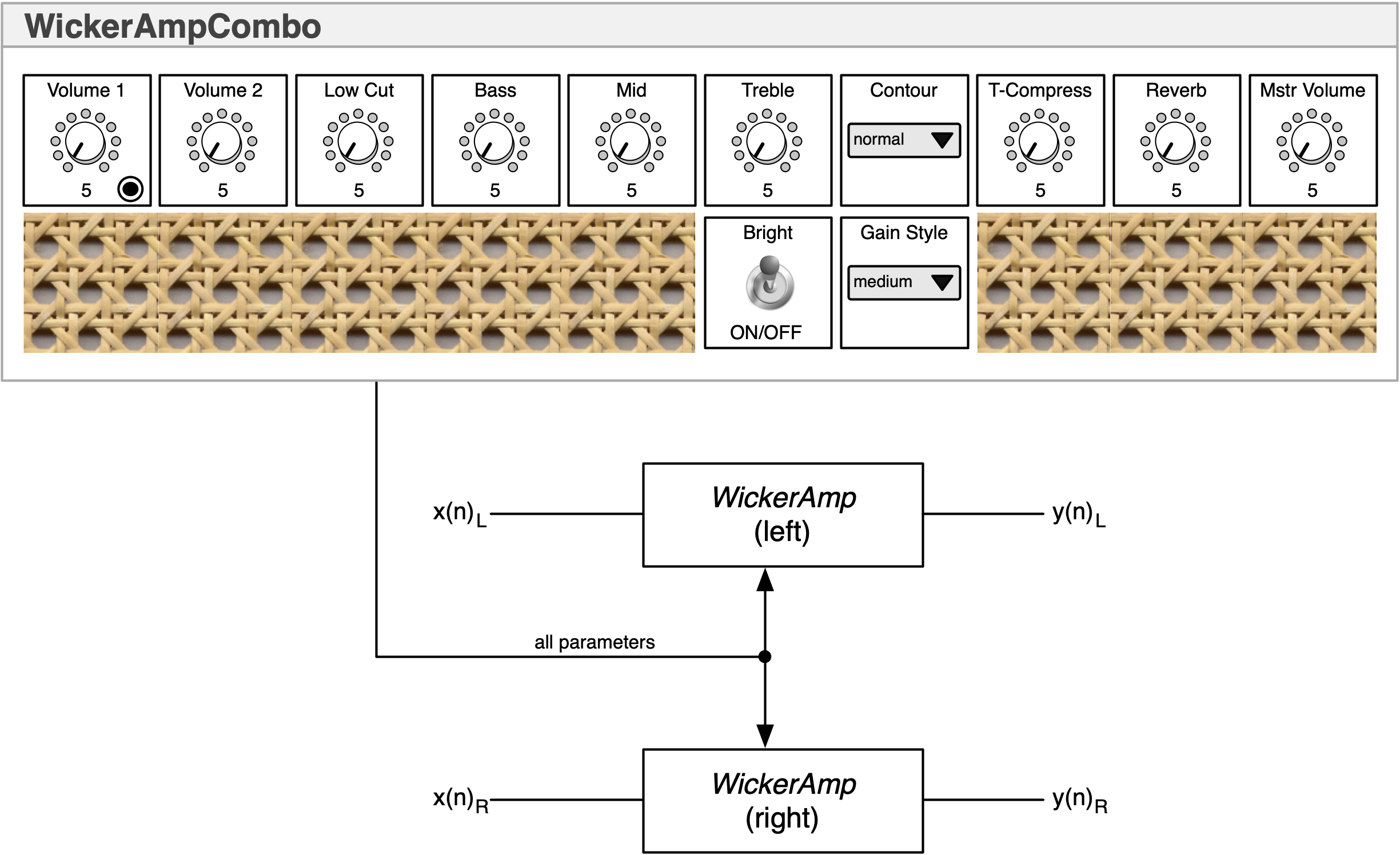
Block Diagram:
Description:
- a complete tube amp simulation from input to output with reverb
Notes:
- see the Chapter 19 addendum for a full description of the plugin and all the details of operation
- emulates 4 Class-A triodes and a Class-B pentode pair
- you can adjust the drive level for the tube-compression in the Class-B model with the “T-Compress” knob
Bonus Video:
Moog Biquad Filter
Chapter 11 Addendum 1: Moog Ladder Filter
Chapter 11 Addendum 1: Moog Ladder Filter
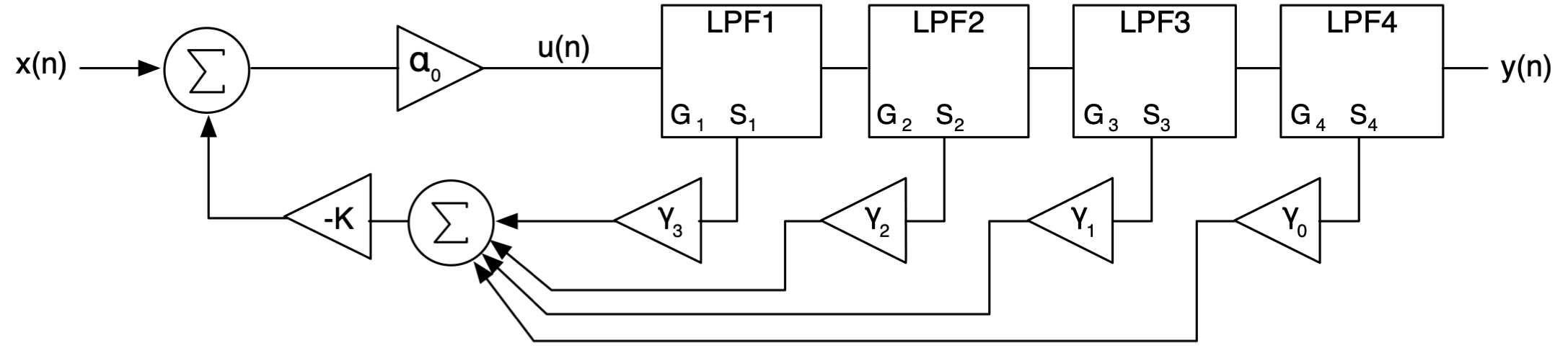
Block Diagram:
Description:
emulation of the classic Moog Ladder Filter with transposed canonical biquad structures
Notes:
- uses the AudioFilter object which defaults to the transposed canonical structure
- you may easily change this in the Biquad object and do listening tests with heavy filter modulation – can you tell the difference?
- the bass boost is not part of the original filter; it is added due to the Moog response (see paper)
